
Pengembaraan Matematik Si Bulus Penjelajah Dengan Algoritma Dijkstra
Pengembaraan Matematik Si Bulus Penjelajah Dengan Algoritma Dijkstra
Penulis: Alyssa April Dellow¹, Prof. Madya Dr. Fatimah Abdul Razak²
¹Calon Doktor Falsafah (Sains Data & Analitik), Jabatan Sains Matematik, Fakulti Sains dan Teknologi di Universiti Kebangsaan Malaysia, UKM.
²Ketua Kumpulan Penyelidikan Rangkaian Kompleks dan Analisis Data Bertopologi (CNTDA)
Jabatan Sains Matematik, Fakulti Sains dan Teknologi
Universiti Kebangsaan Malaysia
Seekor kucing bernama Lana tiba-tiba tersedar bahawa dia perlu segera pulang untuk makan malam bersama-sama kakaknya, Tommy.
“Alamak! Saya dah lambat. Mesti Tommy marah sebab lapar menunggu saya balik,” rungut Lana. Dengan keresahan yang membuak-buak, Lana nekad mencari jalan terpantas untuk pulang.
Namun, misi menjelajah kejiranannya bukan sesuatu perkara mudah memandangkan kawasan kejiranan tersebut mempunyai pelbagai jalan dan tanda pandu yang boleh dilalui.
Lana termenung seketika. Dia teringat bagaimana tuannya pernah melukis peta yang dipenuhi titik-titik kecil yang disambungkan dengan garisan. “Untuk mencari laluan terpendek antara dua titik dalam sesuatu sistem, gunakan algoritma Dijkstra,” kata tuannya ketika itu. Kini, di tengah simpang jalan yang berserabut, Lana rasa seolah-olah dia sendiri berada dalam peta itu.

Peta Kejiranan Sebagai Sebuah Rangkaian
Lana mula membayangkan kejiranannya sebagai sebuah rangkaian. Setiap persilangan jalan diibaratkan sebagai satu nod, manakala jalan yang menghubungkan dua persilangan dianggap sebagai sisi, seperti yang ditunjukkan dalam Rajah 1. Setiap sisi mempunyai berat tersendiri yang mewakili kos perjalanan sepanjang jalan tersebut, contohnya panjang jalan atau masa yang diambil. Rangkaian seperti ini digunakan secara meluas dalam pelbagai jenis bidang untuk menggambarkan secara visual hubungan antara entiti, antaranya rangkaian pengangkutan, kewangan, biologi, sosial dan lain-lain.
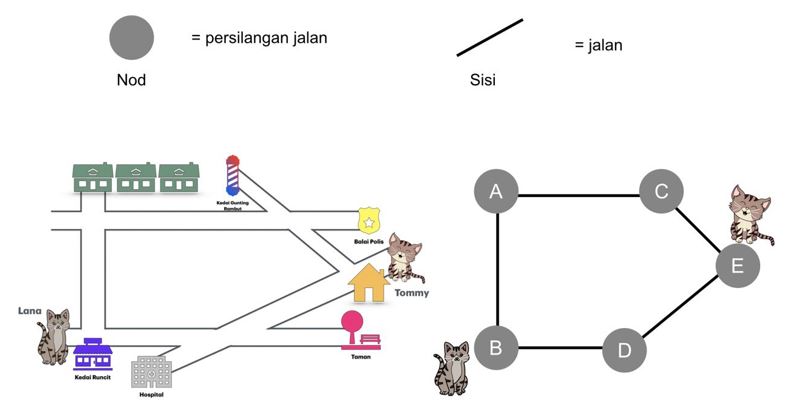
Sumber: Semua rajah dalam artikel ini dihasilkan sendiri oleh pengarang
“Saya Nak Pulang dengan Pantas!”
Lana mula menggunakan strategi berdasarkan algoritma Dijkstra, seperti yang ditunjukkan dalam langkah-langkah berikut. Nombor pada sisi di antara setiap nod mewakili jarak atau kos perjalanan antara persilangan jalan.
1. Lana berada di nod B dan perlu pulang ke nod E, rumah mereka di mana Tommy menunggunya. Jarak dari B ke B ialah 0, manakala jarak dari B ke semua nod lain ditetapkan sebagai infiniti, ∞, (sangat jauh) pada awalnya
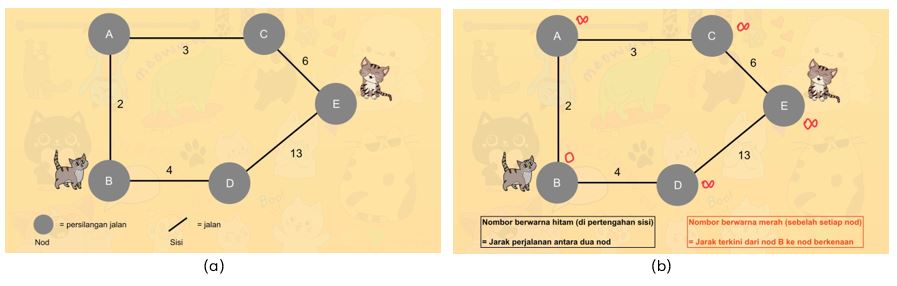
2. Oleh sebab Lana berada di B, nod ini dianggap telah dilawati. Kini, hanya dua nod yang terhubung secara terus kepada B, iaitu A dan D. Kedua-dua nod ini dipertimbangkan sebagai destinasi seterusnya dan diletakkan dalam baris gilir keutamaan.
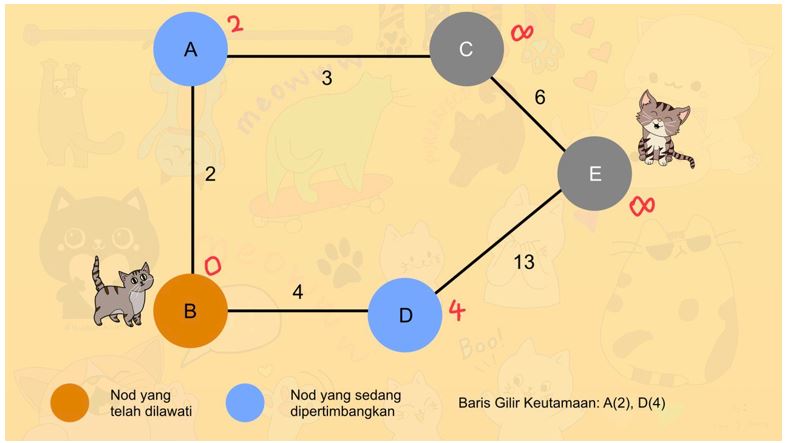
3. Lana memilih nod A sebagai destinasi seterusnya kerana jarak ke A, iaitu 2, lebih pendek berbanding jarak ke D, iaitu 4. Nod A ditandakan sebagai dilawati. Langkah 2 dan 3 diulang, Lana meletakkan nod paling hampir yang belum dilawati dalam baris gilir keutamaan.
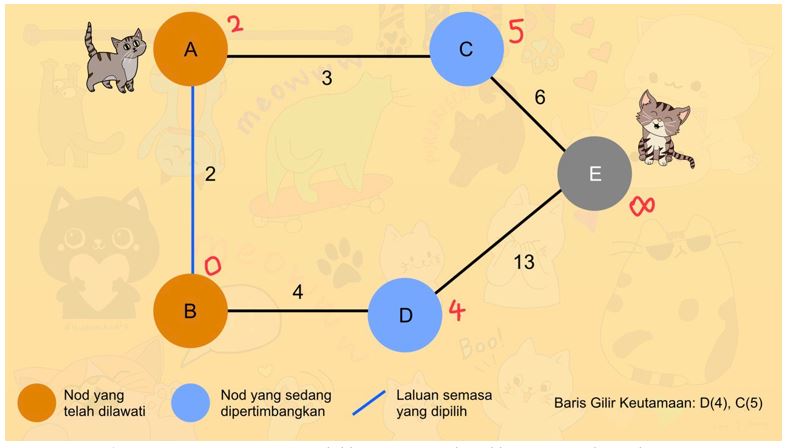
4. Jarak dari tempat asal Lana ke C melalui A ialah 5, tetapi jarak dari B ke D masih kekal 4. Maka, D dipilih terlebih dahulu. Seterusnya, nod C dan E dipertimbangkan.
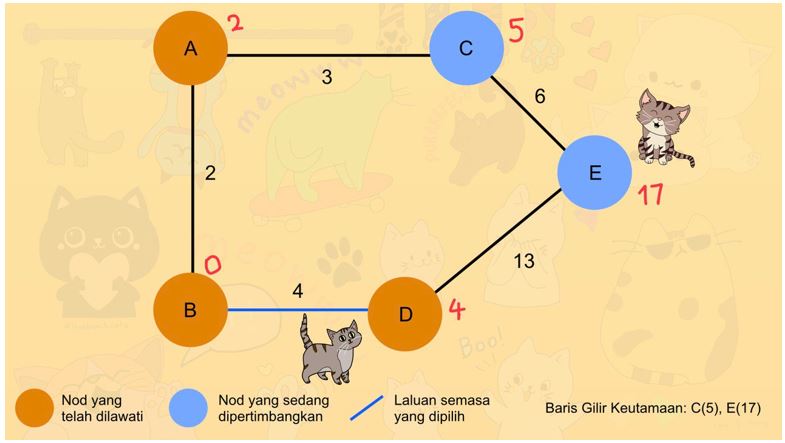
5. Jarak dari B ke C melalui A ialah 5, jauh lebih kurang berbanding melawati E dari D dengan jarak 13. Oleh itu, C dipilih dan ditandakan dilawati.
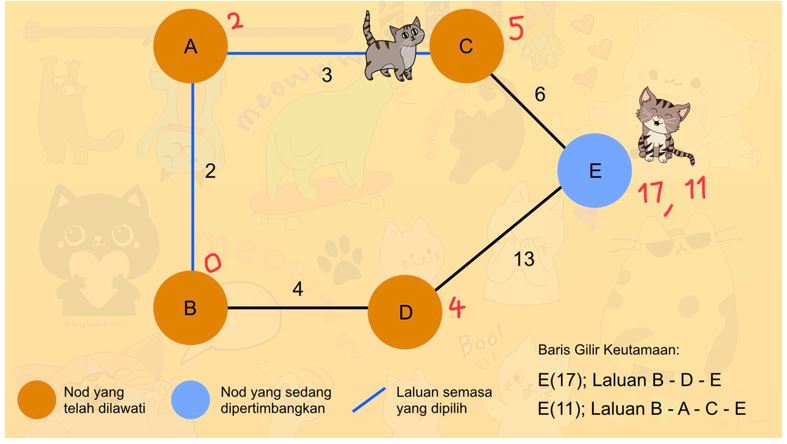
6. Sekarang, Lana perlu membuat pilihan terakhir. Dia membayangkan dua laluan yang tersedia:
-
- B -> D -> E dengan jumlah jarak 17
- B -> A -> C -> E dengan jumlah jarak 11
Walaupun laluan B -> A -> C -> E kelihatan lebih jauh kerana perlu melalui lebih banyak nod dan sisi, sebenarnya laluan ini jauh lebih singkat. Justeru, Lana memilih laluan tersebut sebagai laluan paling optimum!
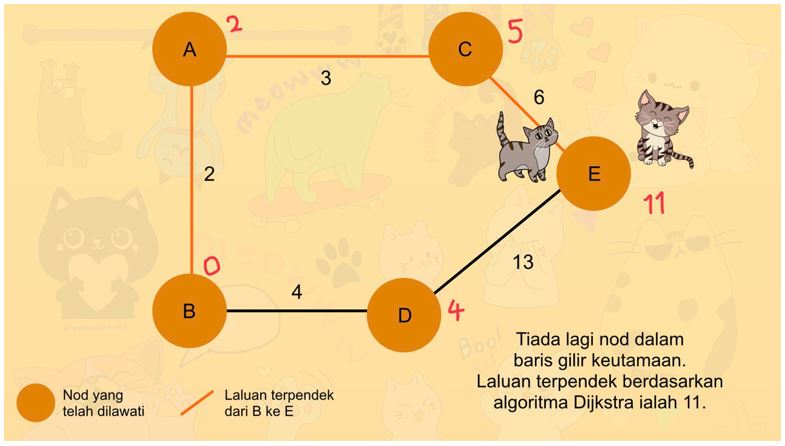
“Wah, saya sempat sampai rumah sebelum Tommy marah. Sekarang kami boleh makan malam dengan tenang.”
Aplikasi Laluan Terpendek dalam Kehidupan Seharian
Walaupun Lana seekor kucing yang bijak, algoritma Dijkstra dan konsep laluan terpendek pada hakikatnya banyak digunakan dalam kehidupan seharian. Contohnya:
- Sistem GPS seperti Google Maps yang mengira laluan terpantas ke destinasi.
- Penghalaan rangkaian (network routing) yang menentukan laluan paling cekap bagi paket data untuk bergerak dari sumber ke destinasi.
- Pengoptimuman logistik seperti merancang laluan penghantaran paling cekap untuk perkhidmatan pengangkutan atau kurier.
Untuk lebih memahami konsep ini, anda boleh menonton video satu minit yang saya sediakan dalam Bahasa Inggeris di bawah.
Sebenarnya, saya tidak sangka bahawa video yang saya hasilkan kerana minat saya terhadap rangkaian (dan kucing!), boleh memenangi anugerah video satu minit terbaik di NetSciX 2025 pada Januari 2025. Sejak tahun terakhir sarjana muda lagi saya terlibat dalam penyelidikan rangkaian kewangan. Pada tahun 2024, saya mendaftarkan diri sebagai pelajar Doktor Falsafah di Universiti Kebangsaan Malaysia dan mula meletakkan fokus penyelidikan saya dalam bidang Sains Rangkaian. Di sinilah saya mula berkenalan dengan Network Science Society, komuniti antarabangsa yang menganjurkan dua persidangan utama setiap tahun, NetSci dan NetSciX. NetSci merupakan persidangan perdana Network Science Society yang menghimpunkan penyelidik Sains Rangkaian dari seluruh dunia untuk bengkel, pembentangan dan pertukaran idea, manakala NetSciX ialah versi musim sejuk yang lebih kecil untuk meluaskan jangkauan NetSci ke lokasi-lokasi lain.
Disebabkan saya dan Dr. Fatimah berpeluang menghadiri NetSciX 2025 di Indian Institute of Technology, Indore, India, saya mengambil keputusan untuk menyertai pertandingan video satu minit dalam menerangkan konsep Sains Rangkaian. Saya sungguh teruja apabila video pemenang dengan suara kartun saya dimainkan di skrin besar. Ramai yang ketawa dan bertanya sama ada itu suara saya atau AI, dan ya, itu memang suara saya yang dilajukan. Momen ini membuka mata saya bahawa matematik boleh dihidangkan secara santai dan bercerita, malah boleh dinikmati oleh pelbagai lapisan masyarakat. Justeru terhasilah artikel ini, disuaikan untuk pembaca tempatan.

Matematik Ada di Mana-mana!
Sudah tentu, Edsger W. Dijkstra tidak menyangka bahawa algoritma ciptaannya pada tahun 1956 akan digunakan secara meluas, malah turut “digunakan” oleh seekor kucing untuk mencari jalan pintas! Jika anda rasa sesuatu masalah matematik terlalu sukar, cuba pecahkan konsep kompleks tersebut kepada bahagian-bahagian kecil yang mudah difahami. Matematik membantu menyelesaikan masalah rumit secara teratur dan boleh diaplikasikan dalam pelbagai teknologi moden.
Jadi, lain kali anda sesat dan menggunakan GPS, ingatlah algoritma Dijkstra. Malah, anda boleh cuba sendiri dengan melukis rangkaian ringkas kejiranan anda dan menggunakan algoritma Dijkstra untuk mencari laluan terpendek dari satu sumber ke destinasi. Jika seekor kucing boleh memahaminya, anda juga boleh!
Bagi pembaca yang berminat meneroka konsep Sains Rangkaian yang lain pula, khususnya bagaimana konsep-konsep ini muncul dalam rangkaian media sosial, anda boleh membaca artikel “Like, Komen, Share dan Hubungannya dengan Matematik” kami di Majalah Sains.
Rujukan dan Pautan
Alyssa April. 2024. A Cat’s Quest for the Shortest Path Using Dijkstra’s Algorithm. YouTube. https://www.youtube.com/watch?v=cQXnsD33_7s [9 Jun 2025].
Alyssa April Dellow & Prof. Madya Dr. Fatimah Abdul Razak. 2025. Like, Komen, Share dan Hubungannya dengan Matematik. Majalah Sains. https://www.majalahsains.com/like-komen-share-dan-hubungannya-dengan-matematik/ [21 Oktober 2025].
Centrum Wiskunde & Informatica (CWI). t.th. Edsger W. Dijkstra: Brilliant, colourful, and opinionated. https://www.cwi.nl/en/about/history/e-w-dijkstra-brilliant-colourful-and-opinionated/ [9 Jun 2025].
Dijkstra, E.W. 1959. A Note on Two Problems in Connexion with Graphs. Numerische Mathematik 1: 269-271. https://ir.cwi.nl/pub/9256/9256D.pdf [22 September 2025].
GeeksforGeeks. 2025. Applications of Dijkstra’s shortest path algorithm. http://geeksforgeeks.org/dsa/applications-of-dijkstras-shortest-path-algorithm/ [8 Jun 2025].
Indian Institute of Technology, Indore, India. t.th. NetSciX 2025: International School and Conference on Network Science. https://netscix2025.iiti.ac.in/ [9 Jun 2025].
NetSci. t.th. The Network Science Society. https://netscisociety.net/home [27 September 2025].







